Cells as Random Walkers

Model

The goal is to simulate a connected, one-dimensional chain of freely diffusing cells. We model the chain of cells by only worrying ourselves with the edges of each cell since we are interested in the case where all the edges are touching. Each edge can be modeled as an independent random walker with the following to constraints.

1. The distance between each walker must always be larger than some minimum distance in order to represent the minimum size of each cell. The distance between each walker must also stay smaller than some maximum distance in order to represent the finite size of each cell.
2. The walkers may not overlap nor hop ahead of one another since this would represent the case of cells overlapping each other.

Results

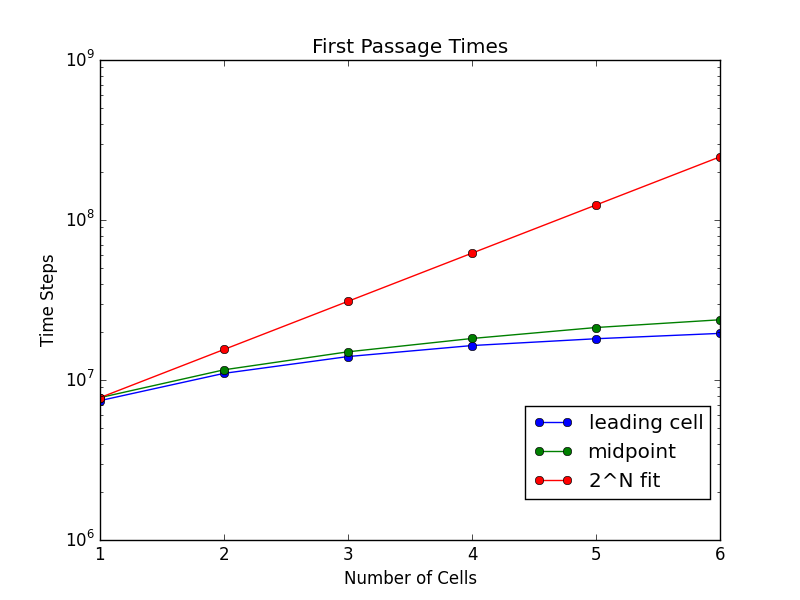
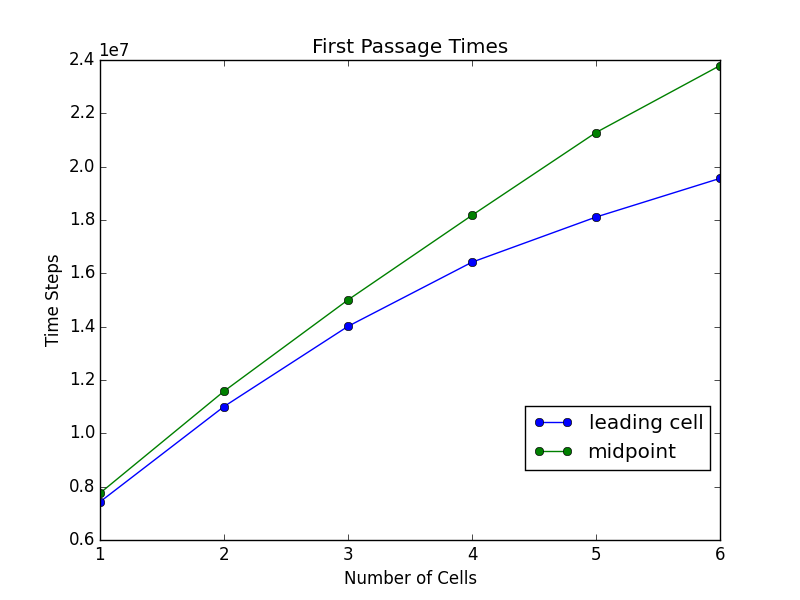
Mean First Passage Times

The following plots show the mean first passage times for simulations as the number of cells is varied. The mean passage times were calculated from 500 individual runs. The other parameters remained fixed between simulations.

Implementation

For a simulation of N cells, N+1 random walkers are initialized.

    d = int((dmax-dmin)/2) + dmin
    rw(:) = 0
    do j = 2, N
        rw(j) = rw(j-1) + d
    enddo

The walkers freely move each time step until the group of cells reaches the absorbing boundary.

    do while( runCheck /= 1 )
        tstep = tstep + 1

        rwOld = rw
        call walkstep( rw, N)

We make sure that the cells stay within the simulation space and also do not hop over one another.

        do j = 2, N
        
            ! check for overlap and hopping
            if( rw(j) <= rw(j-1) )then
                rw(j) = rwOld(j)
                rw(j-1) = rwOld(j-1)
            endif
            
            ! check distance between walkers
            d = rw(j) - rw(j-1)
            if( (d < dmin) .OR. (d > dmax) )then
                rw(j) = rwOld(j)
                rw(j-1) = rwOld(j-1)
            endif
            
        enddo

We then check our criteria for completing a run. In this case it is when the midpoint of the group of cells first passes the absorbing boundary.

        if( rw(1)+int((rw(N)-rw(1))/2) == absbd )then
            runCheck = 1
        endif

The subroutine walkstep choose the direction of the random walk of each walker.

subroutine walkstep( rw, N)
    implicit none
    integer, intent(in) :: N
    integer, dimension(:), intent(inout) :: rw
    integer :: j
    real :: r

    ! execute random walk
    do j = 1, N
        call random_number(r)
        if( r <= 0.5 )then
            rw(j) = rw(j) + 1
        else
            rw(j) = rw(j) - 1
        endif
    enddo
end subroutine walkstep