Lecture 6
Lipid Geometry
What determines the shape of grouped lipids?

Micelle
A good guess is that conical shaped lipids are more likely to form micelles. Let a cone-shaped lipid have a length \(l\), circular surface area \(a\) and total volume \(v\). Using these assumptions we can calculate the number of lipids \(N\) that fit in a micelle of radius \(R\).
\[N = \frac{4\pi R^2}{a} = \frac{\frac{4}{3}\pi R^3}{v} \\ \Rightarrow R = \frac{3v}{a}\]Lets restrict \(R<l\) since we want the lipids packed tightly together such that no water is in the center of the micelle.
\[\rightarrow \frac{3v}{a} < l \\ \text{Sphere Regime:} \\ \frac{v}{al} < \frac{1}{3}\]This dimensionless quantity \(v/al\) is referred to as the shape factor of the lipid. Different shape factors results in different shaped lipids which in turn tells us what kind of form a group of those lipids will take.
Cylinder
Imagine grouping lipids together such that they form a cylinder. We can calculate the number of lipids \(N\) in that cylinder of length \(L\) and radius \(R\).
\[N = \frac{2\pi RL}{a} = \frac{\pi R^2 L}{v} \\ \Rightarrow R = \frac{2v}{a} < l \\ \text{Cylinder Regime:} \\ \frac{1}{3} \lesssim \frac{v}{al} \lesssim \frac{1}{2}\]Bilayer
For a bilayer with surface area \(L^2\) and depth \(2R\):
\[N = \frac{2 L^2}{a} = \frac{L^2 2R}{v} \\ \Rightarrow \frac{v}{al} = 1 \\ \text{Bilayer Regime:} \\ \frac{1}{2} \lesssim \frac{v}{al} \lesssim 1\]Inverted Micelle

An inverted micelle occurs in the regime with the largest shape factor.
\[\text{Inverted Micelle Regime:} \\ 1 \lesssim \frac{v}{al}\]Typical Lipid
\[a \approx 0.5 \text{nm}^2 \\ l \approx 1.3 \text{nm} \\ v \approx 0.6 \text{nm}^3 \\ \Rightarrow \frac{v}{al} \approx 0.8\]Therefore the typical grouped lipid shape is a bilayer.
Problems with Bilayers
- In the form of a single sheet, the edges are exposed which is energitically unfavorable.
- This is quantified with an Exposure Energy.
- In the form of a spherical surface, there are no edges so this penalty is avoided. However, now there is an energy penalty due to the bending of the lipids.
- This is quantified with a Binding Energy.
Exposure Energy
Define \(\lambda\) as the line tension of the exposed side of a bilayer. \(\lambda\) has units of energy per length. So we can set the exposure energy as the following:
\[\rightarrow E=\lambda L\]Bending Energy
Define \(C\) as the curvature of the bilayer. We can relate the radius of the curved bilayer to the curvature through the following expression:
\[C = \frac{1}{R}\]The curvature can lie within the range \(0 \leq C \leq \infty\), and \(0\) corresponds to a flat bilayer whereas \(\infty\) corresponds to a sharp kink in the bilayer.
For a two dimensional surface - like a bilayer - there are two ways it can curve and so the bending energy has to take that into account. For bilayers this is usually expressed in terms of energy per unit area in the following way:
\[\frac{E}{A} = \frac{B}{2} \left( \frac{1}{R_1} + \frac{1}{R_2} \right)^2 + G \frac{1}{R_1 R_2}\]\(B\) and \(G\) are parameters with units of energy which depend on the type of lipid bilayer. We can simplify this expression for the case of a spherical and cylindrical bilayer.
\[\text{Spherical Surface: } R_1 = R_2 \\ \frac{E}{A} = \frac{1}{R^2} (2B+G) \\ \text{Cylindrical Surface: } R_1=R, \ R_2 = \infty \\ \frac{E}{A} = \frac{\pi BL}{R}\]Disk vs Sphere Comparison
Let the surface area of a flat disk shaped bilayer be equal to the surface area of a spherical bilayer (vesicle).
\[A = \pi (2R)^2 = 4\pi R^2\]The two bilayers will have the following binding energies:
\[E_{\text{disk}} = 4\pi\lambda R \\ E_{\text{sphere}} = 4\pi (2B+G)\]Since \(E_{\text{sphere}} < E_{\text{disk}}\) a vesicle will form because it is energetically favorable.

\(\lambda_\text{min}\) is the minimum line tension for which the above inequality holds. For typical bilayers at room temperature \(\lambda_\text{min} = 10^{-13} \text{J}/\text{m}\) and line tension has been observed to be on the order of \(10^{-11}\text{J}/\text{m}\).
However, in this discussion we have not considered the entropy cost of such configurations. The bilayer sheet has higher entropy than the sphere since the positions the lipids can take in a vesicle are much more constrained. In order to account for this lets assume that the line tension is actually a function of lipid length and temperature.
\[\rightarrow \lambda_\text{min} \approx f(b,T) \\ \lambda_\text{min} = \frac{kT}{b}\]For typical lipid chain lengths of 4nm this leads to a \(\lambda_\text{min} \approx 10^{-12}\text{J}/\text{m}\).
Closed Bilayer Shape
What shape does a closed bilayer (vesicle) take from binding energy considerations alone?
Consider a vesicle with volume \(V\) which is less than the volume of a sphere \(V_\text{sph}\) but that has surface area equal to a sphere, \(A = A_\text{sph}\).
Reduced Volume
We create a unit less measure called the reduced volume. The goal is to have a unit less measure that compares an objects volume and surface area. Hence, the reduced volume should have the following form in order to be dimensionless.
\[\Rightarrow \frac{V}{A^{3/2}} \\ \text{For a sphere: } \frac{V}{A^{3/2}} = \frac{1}{6\sqrt{\pi}}\]Lets normalize the measure by the resulting ratio for a sphere. So the reduced volume \(\bar{V}\) is defined as
\[\bar{V} \equiv \frac{6\sqrt{\pi}V}{A^{3/2}}\]Note that the reduced volume ranges \(0 \leq \bar{V} \leq 1\). Now lets calculate the reduced volume \(\bar{V}\) for different shapes.
Spherocylinder (Rod)
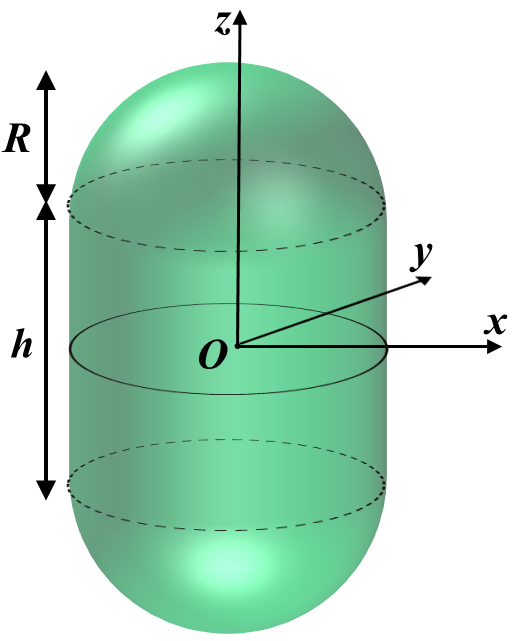
In our case let \(h \rightarrow L\) and define \(l \equiv L/R\).
\[\bar{V} = \frac{4+3l}{\sqrt{2}(2+l)^{3/2}} \\ \text{If } l=0 \Rightarrow \bar{V} = 1 \\ \text{If } l>>1 \ \ \ \Rightarrow \bar{V} \approx \frac{3}{\sqrt{2l}}\]Lets define \(\Delta\bar{E} \equiv \Delta E / B\). Now let us calculate the bending energy and compare it to that of a sphere.
\[\Delta E = E - E_\text{sph} = \frac{\pi BL}{R} \\ \Delta \bar{E} = \pi l \\ \Rightarrow \bar{V} \sim \frac{1}{\Delta \bar{E}^{1/2}}\]Written with StackEdit.
