Phase Space

We vary the parameters \(\beta\) and \(\epsilon\) and observe the resulting mean first passage time. Other parameters are left fixed unless otherwise noted, all plots are of groups of 4 cells.

No Perimeter Energy Constraint

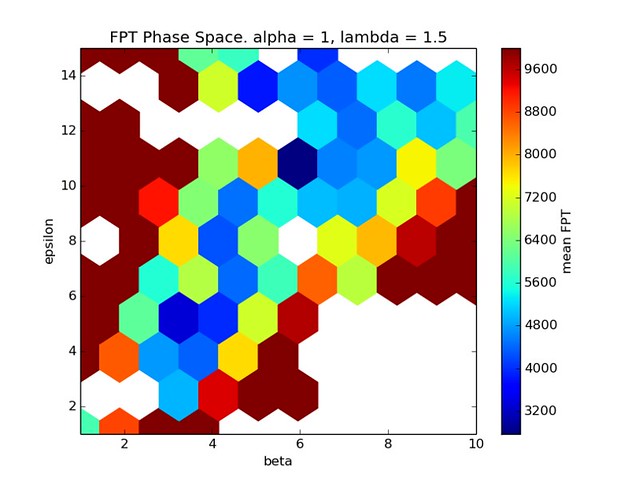
Above is the resulting phase space for simulations in which there is no constraint on the perimeter length of cells. Since there is no perimeter constraint, cells are allowed to stretch into long-stringy shapes which are not biologically relevant.

From the plot we see that FPT is at a minimum for a ratio of \(\beta\) and \(\epsilon\) equal to a little more than 1 . If \(\epsilon > \beta\) then cell polarization strength is very strong and works to pull the group of cells apart causing FPT to increase. In the case of \(\epsilon < \beta\) the energy cost of the cell moving into the ECM is too large resulting in very slow net movement of the group.

Perimeter Energy Constraint

Although we can optimize parameters to get short FPT, in all cases the cells tend to stretch-out into unphysical shapes. In order to prevent this from happening we add a perimeter energy contraint term to the Hamiltonian of the form

\[\lambda_P (P - P_0)^2 \ .\]

This will make it energetically favorable for cells to retain circle-like shapes.

Strong Perimeter Constraint

In this case we have set \(\lambda_P = 0.1\).

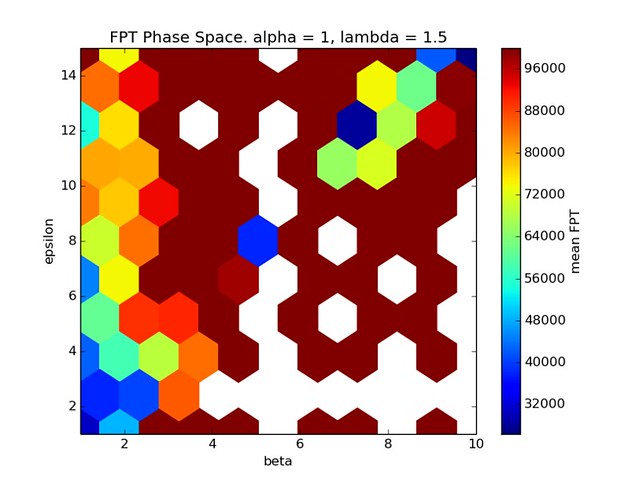
The FPT data has been scaled such that 100,000 time steps is the max value represented in the heat map.

In this case it seems that there are two separate regions of minimal FPT. One occurs at low values of for both parameters. The other is again for ratio a of \(\beta\) and \(\epsilon\) equal to a little more than 1, but only for sufficiently large values of both parameters.

Lets explore what the cell dynamics actually look like for different regions on this phase space. I hope you like pink!

For \(\beta = 1.5\) and \(\epsilon = 2.0\)

For \(\beta = 2.0\) and \(\epsilon = 11\)

For \(\beta = 8.0\) and \(\epsilon = 13\)

Weak Perimeter Constraint

In this case we set \(\lambda_P = 0.01\), ten times smaller than the previous case.

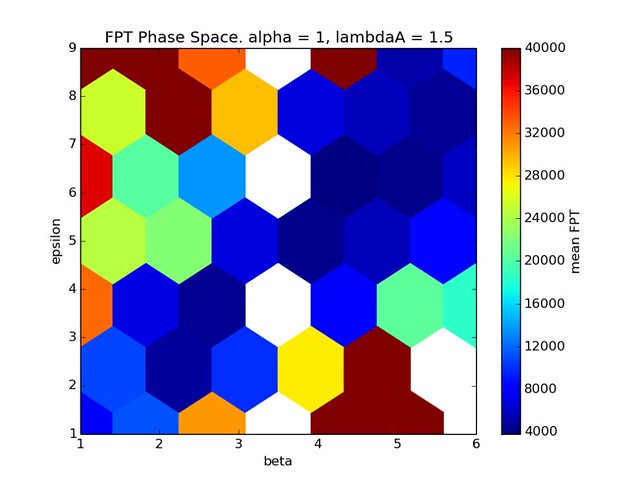
The resulting phase space looks much more like the original, no perimeter constraint result. Again, for a ratio of \(\epsilon\) to \(\beta\) of a little more than one the FPT is minimized. Like the other simulations, when \(\beta\) is too large the FPT increases since movement into the ECM becomes energetically unfavorable. When \(\epsilon\) is too large the group of cells is torn apart decreasing cell’s ability to sense its environment.

Lets look at the cell dynamics for different parameter values in the phase space.

For \(\beta = 2.00\) and \(\epsilon = 2.0\)

For \(\beta = 2.0\) and \(\epsilon = 8.0\)

For \(\beta = 5.5\) and \(\epsilon = 8.0\)

Julien Varennes

Written with StackEdit.