Simulation Set-up

• Reflective boundary on the left.
• Absorbing boundary on the right.
• Cells are always connected, cells may stretch and contract.
  • The number of cells is varied.
  • The amount by which a cell can stretch is varied.
    • cellstretch refers to the maximum number of additional lattice points a cell may occupy.
• Cells are initialized along the reflective boundary and all only occupy one lattice point.

Mean First Passage Time

Hypothesis

• The mean passage time will increase exponentially as the number of cells in the simulation increases.
• The strength of the exponential will decrease if the cells are allowed to stretch more.

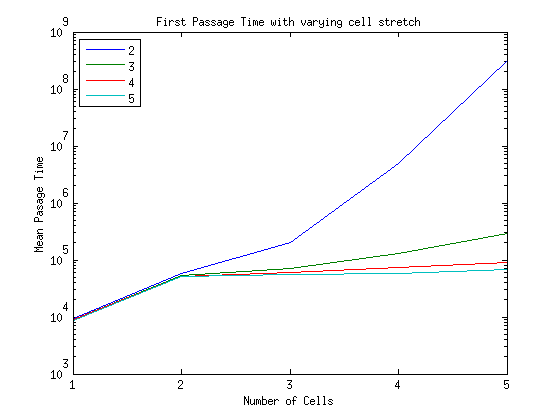
Results

The box indicates the value of cellstretch for that set of data.

• In the one cell case we recover the same result as the single cell diffusion simulations. The mean passage time is \(10^4\) time steps.
• For \(N=2\) to \(N=5\) our hypothesis seems to be on the right track.
  • I am unsure as to the cause of the kink in the exponential increase which occurs at \(N=2\) for all cases.
    • I believe it has something to do with the fundamental difference between 1 and multiple cell diffusion. When \(N\geq2\) then the cells must stay connected and diffuse together whereas in the 1 cell case there is no such constraint.
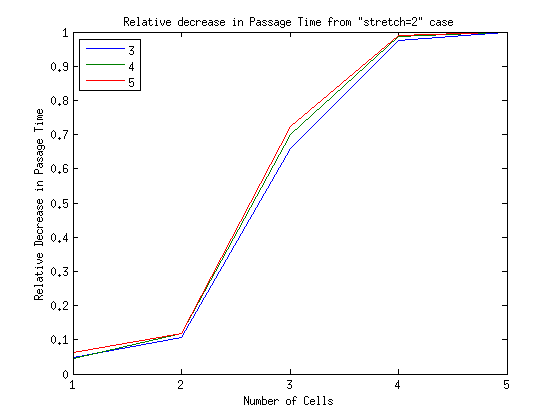
• Our hypothesis that increasing cellstretch will decrease the strength of the exponential increase is incorrect.
  • I am surprised by how the benefit of being able to stretch more quickly decreases.

Below is the relative decrease in mean passage time with respect to the cellstretch = 2 case.

Written with StackEdit.