Cell Volume as a function of Alpha

Model

\[\beta H_s = \sum_{j=1}^N \left[\alpha\left(V_j/V_0-1\right)^2-\sigma_j\gamma\right]\]

A simple check that the simulations are working is to see how the cell volume \(V_j\) changes as \(\alpha\) changes.

We expect that for large values of \(\alpha\) energy costs for stretching and compression are high and so the cell will stay near the relaxed volume. Whereas when \(\alpha\) decreases the spread in cell volume will get larger.

Results

All results were done with \(\gamma=10.0\) and a simulation space of 1,000 lattice points.

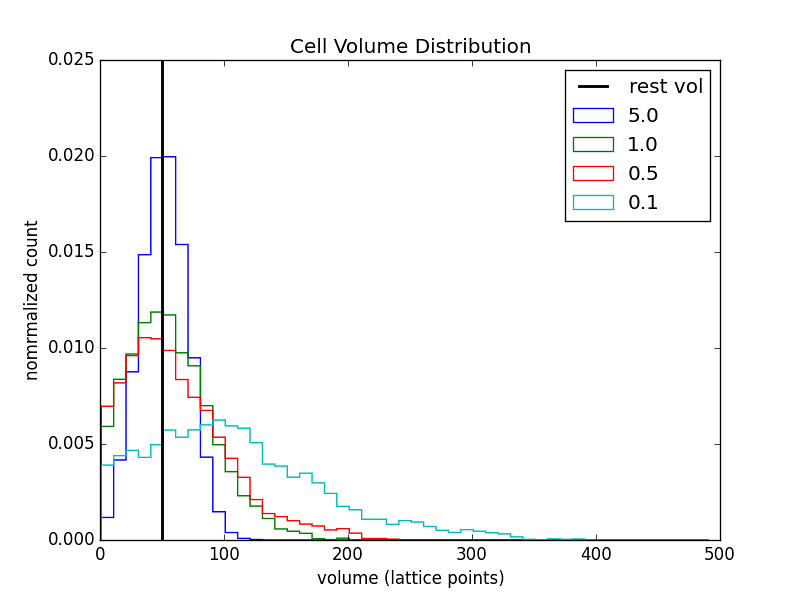
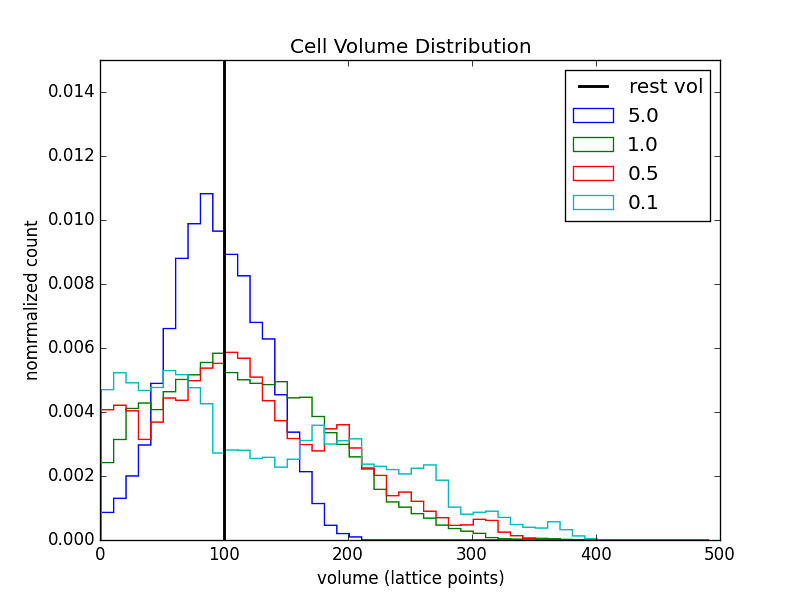
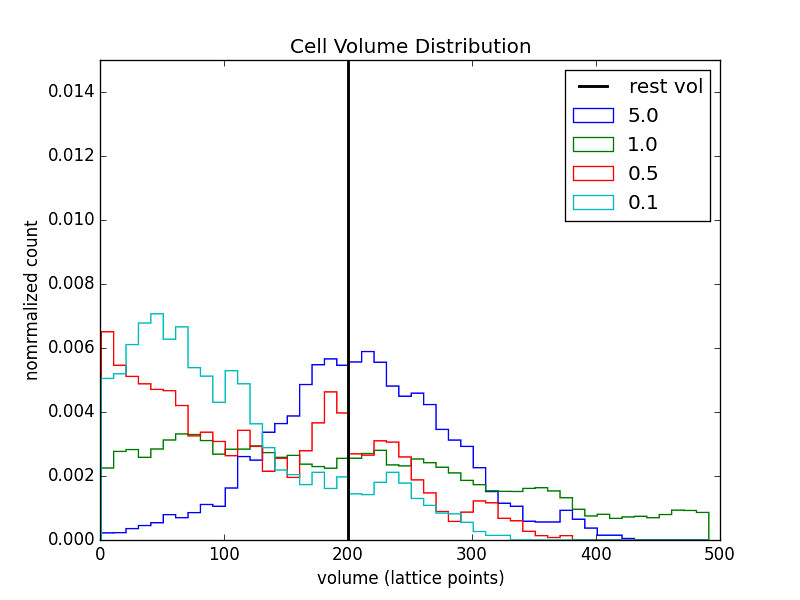
1 Cell Chain

The legend indicates the value of \(\alpha\) for the respective run.

The relaxed volume size (black bar) was varied as well.

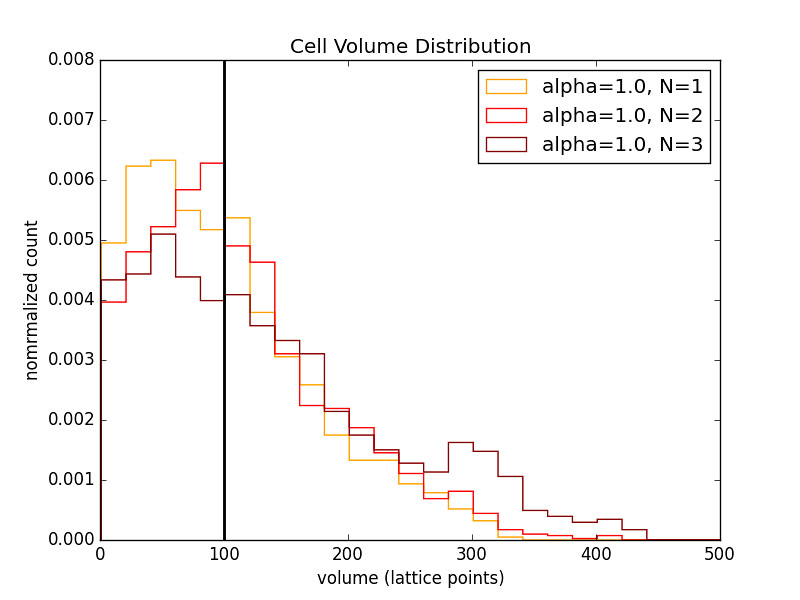
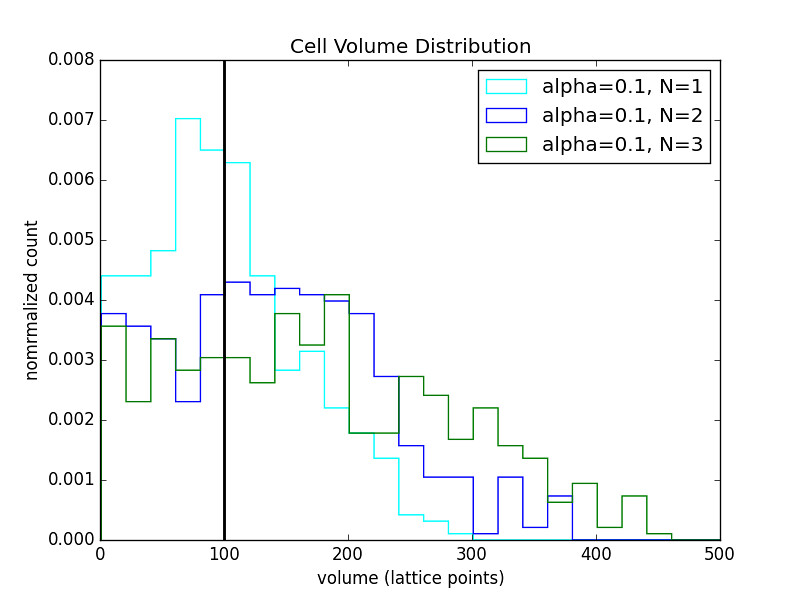
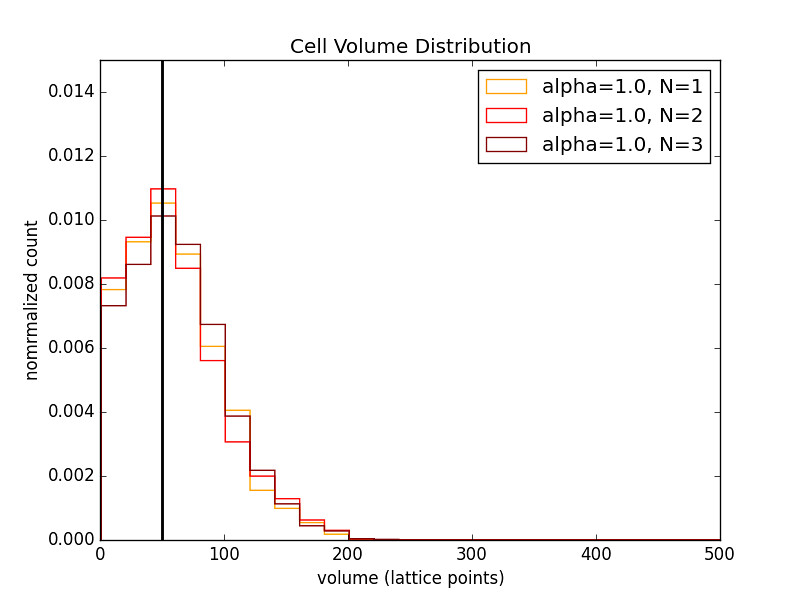
3 Cell Chain

The legend indicates the cell in the chain. They are numbered from the reflective boundary out.

The relaxed volume size (black bar) was varied as well.

Observations

• As alpha increases the distributions become more sharply peaked about the relaxed cell volume.
• As alpha decreases the distributions become wider.
  • As alpha gets smaller the symmetry in the distribution is broken by the fact that the volume cannot get smaller than 1.
• Relaxed cell volume does have an effect on the distribution.
  • As \(V_0\) increases the distribution becomes more spread out.
    • This makes sense since changes in \(V_j\) will now lead to smaller changes in the quantity \(\left(V_j/V_0-1\right)^2\)
    • And so the energy cost for stretching/compression decreases.
    • Making the relaxed volume large gives the benfit of a more symmetric distribution but at the cost of widening that distribution for all values of alpha.

It seems that having a small relaxed volume is more beneficial than a large one. With \(V_0=50\) the distributions keep more of their desired shape even for small \(\alpha\).