1 Cell Diffusion with No State Switching

$$ P(x|t) $$

Prediction

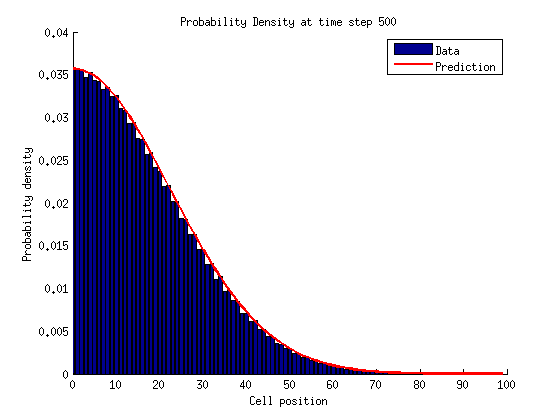
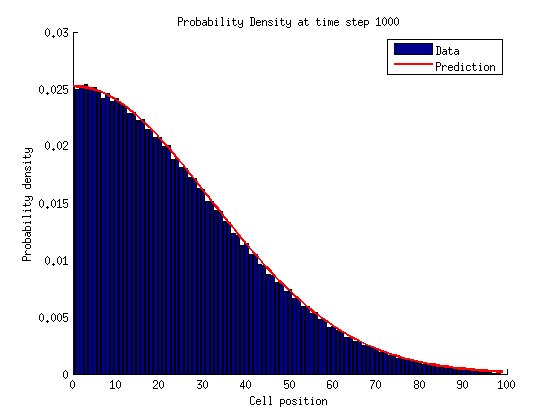
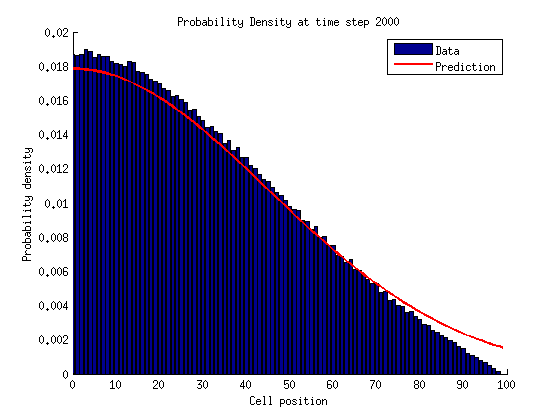
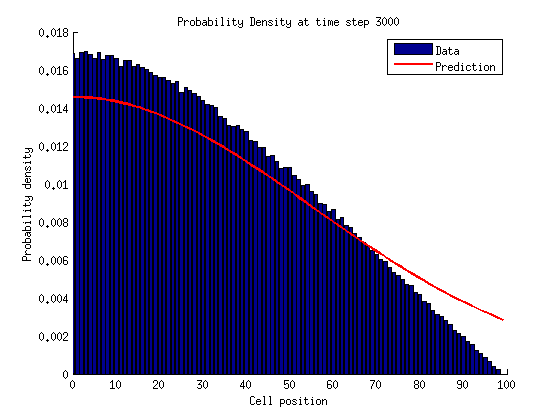
The probability density for cell location given a time \(t\) should look like a normal distribution. As time increases this prediction becomes less accurate since more and more particles get absorbed at the right side boundary.

\[P(x|t) = \frac{2}{\sqrt{2\pi\sigma^2}} e^{-x^2/2\sigma^2} \\ \sigma^2 = 2Dt\]

The extra factor of two in \(P(x\vert t)\) is because of the reflective boundary at the origin. In an 1D random walk so \(\left<x\right> = 0\), therefore \(\sigma^2 = \left<x^2\right>\), and \(\left<x^2\right> = Nb^2\).

\[\Rightarrow 2Dt = Nb^2 \\ t = N \Delta t \\ \Rightarrow D = \frac{b^2}{2\Delta t}\]

Results

At small times the data is very much inline with prediction.

At large times the data starts to diverge from a normal distribution as more and more cells are absorbed.

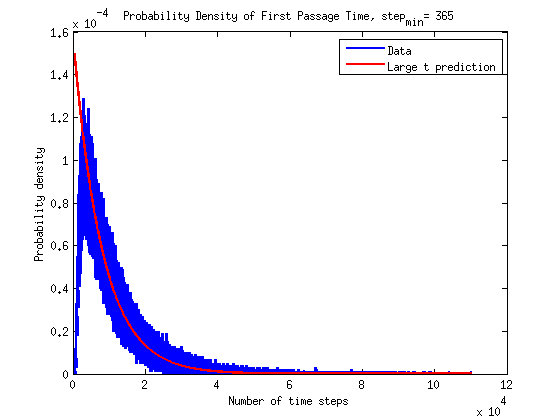
First Passage Time

Prediction

\(P(t)\) is the probability density of the first passage time. It is expressed as the following:

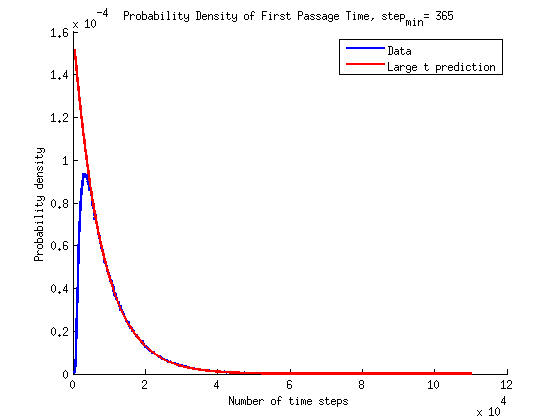
\[P(t) = -D \frac{\partial P(x|t)}{\partial x} |_{x=L}\]

This equation has a solution for our set of initial and boundary conditions. In the large time limit this solution can be expressed as:

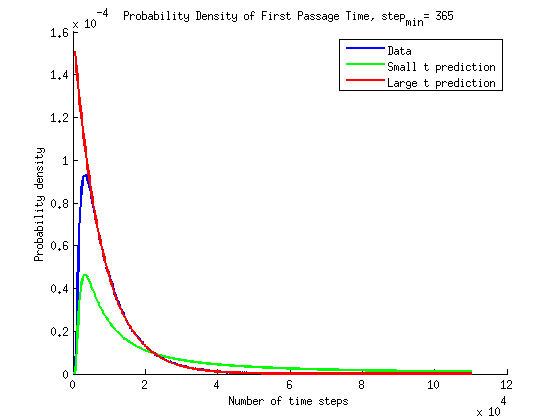
\[P(t) = \frac{2D}{L^2} \sum_{m=1}^{\infty} \beta_m e^{-\beta_m^2 D t / L^2} \sin\left(\beta_m \frac{x}{L}\right) |_{x=L}\]

In the following plots only the first term, \(m=1\), from the series is used.

Update I have added a short time prediction for \(P(t)\) to the plots below. We observed that at short times \(P(x|t)\) looks like a normal distribution. Hence an appropriate approximation for the small time behavior of \(P(t)\) can be calculated from the normal distribution.

\[P(x|t) = \frac{2}{\sqrt{2\pi\sigma^2}} e^{-x^2/2\sigma^2} \Rightarrow \frac{\partial P(x|t)}{\partial x} = \frac{-2x}{\sigma^2\sqrt{2\pi\sigma^2}}e^{-x^2/2\sigma^2} \\\]

Therefore the short time approximation is the following:

\[P(t) = \frac{x}{t\sqrt{2\pi\sigma^2}}e^{-x^2/2\sigma^2} |_{x=L}\]

Results - Update

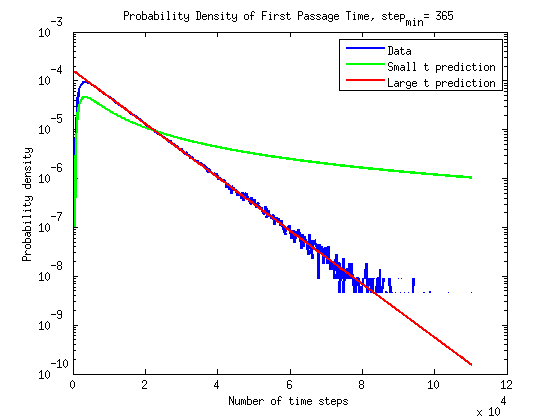
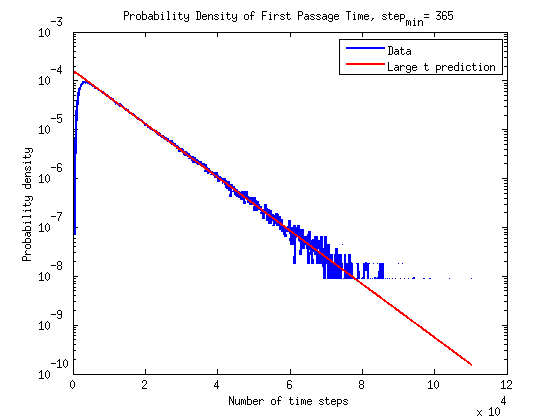
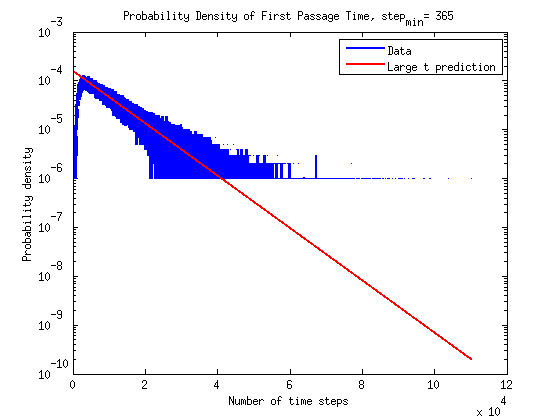
The results are plotted here on a normal scale and on a semilog scale. The prediction at large times does seems to be in agreement with the simulations.

Update 2, I have added the small time prediction to the plots. At small times it does seems to be in agreement with the simulations. The semilog plot illustrates that the the exponential increase in \(P(t)\) is well described by the small time approximation.

Update 1, I have since gone back and remade the plots as a histogram. In creating the histograms I weight the probability density in each bin by the width of the bin to ensure that the whole probability density is properly normalized.

Old Plots I believe the thickness of the band in the data is due in part because of the large time scale plotted and that on small timescales there is lots of variation in the probability density.

Written with StackEdit.