In this post I will investigate the sequencing data from The Cancer Genome Atlas (TCGA) in order to familiarize myself with handling sequencing data. Specifically, I will focus on a dataset which is a subset of somatic mutations found...

Our study of multicellular chemotaxis was recently published in Physical Review Letters. The work compares two typical methods of collective chemotaxis in order to determine which one is more accurate in tracking chemical gradients.

Random walks have been used to study many phenomena in biology and ecology. Here I present a model of a biased and persistent random walk with the goal of using it to study cell chemotaxis.

In...

Research I conducted in conjunction with Prof. Andrew Mugler and Prof. Bumsoo Han has been published today in Biophysical Journal. The paper, Collective Chemotaxis through Noisy Multicellular Gradient Sensing , examines how cell-cell communication can enable a...

Prof. Andrew Mugler and I wrote a review on cancer metastasis from a physics perspective. By using simple physical models the limits to metastatic cells’ sensory capabilities can be understood, and experimental evidence that cells operate near these...

Multicellular Sensing and Migration

As previously discussed cell sensing and communication is modelled using the LEGI framework. The polarization vector \(\vec{p}\) is updated based on the downstream output of the LEGI model and the repulsion vector \(\vec{q}\).

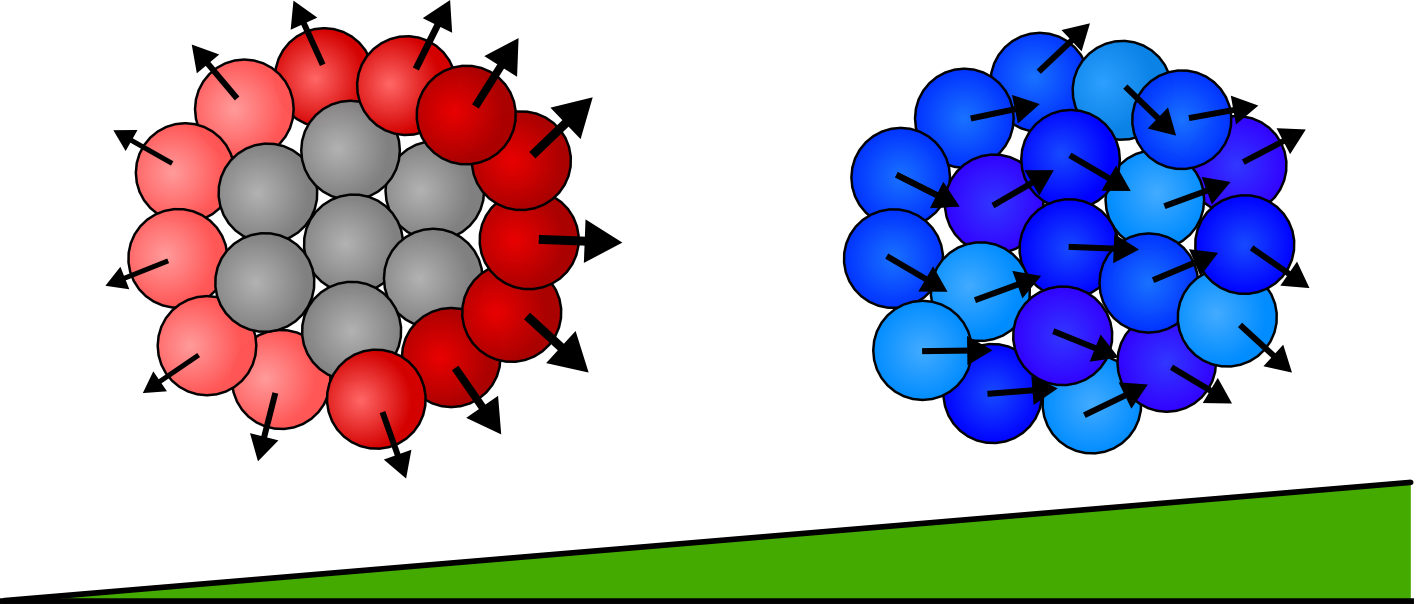
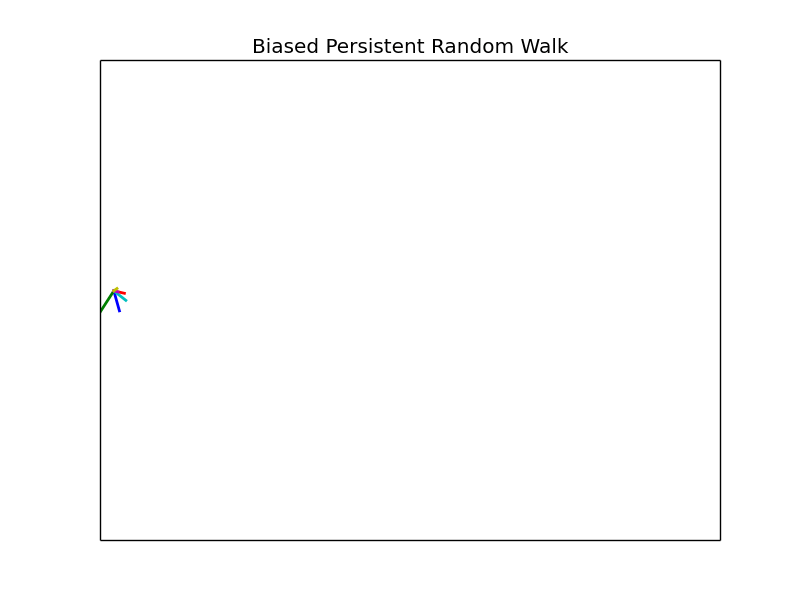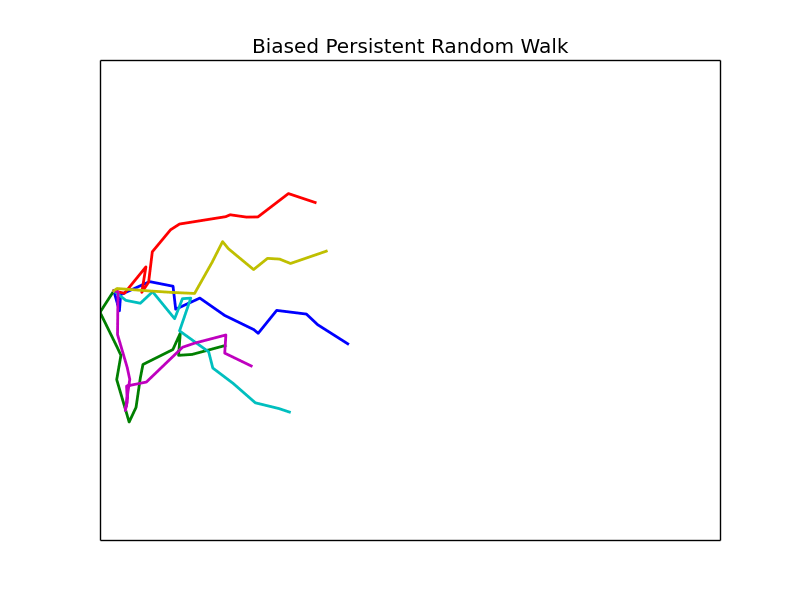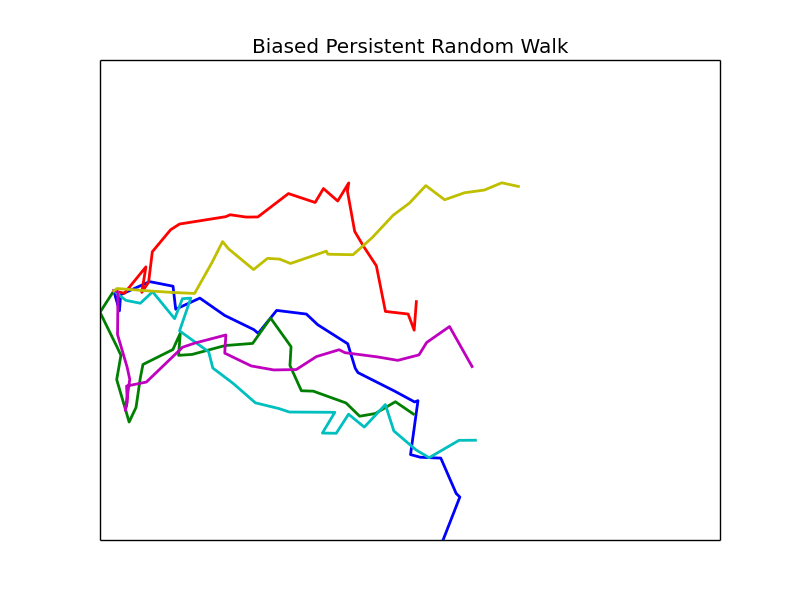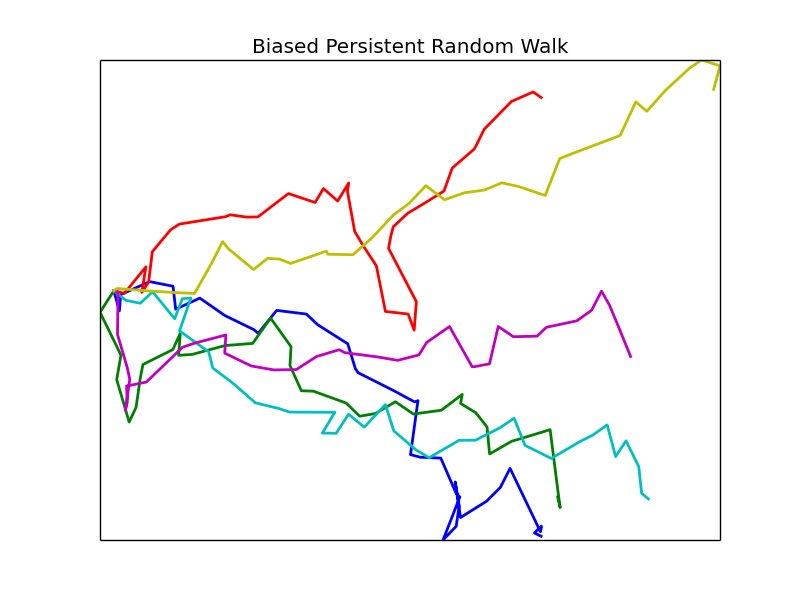
Phase Space

We vary the parameters \(\beta\) and \(\epsilon\) and observe the resulting mean first passage time. Other parameters are left fixed unless otherwise noted, all plots are of groups of 4 cells.

No Perimeter Energy Constraint

Read More

Cell Sensing, Implementation in CPM Code

Overview

Cells in a group communicate with one another in order to sense a gradient. We use a minimal adaptive model based on local excitation and global inhibition (LEGI). The network looks...

Simulation Parameters:

• Each cell has a relaxed area of 27 lattice sites.
  • Cells are initialized as 3x3x3 cubes.
• Each simulation runs for 300 Monte Carlo (MC) time steps.
• Statistics in each case are gathered...

1 Cell

Resting Area of 4 Pixels

The simulation ran for 100 different instances each for a maximum of 60 Monte Carlo (MC) time steps.

From the simulations we were able to get statistics on the mean square...

Adaptation

We will continue our discussion on adaptation from the last lecture. We want to answer the question of what causes the sharp decrease (response) in activity \(A\) due to an increase in ligand concentration \(l\).

Response Curve

Bacteria Forward Motion & Tumbling

As previously discussed, most bacteria use flagella in order to achieve forward motion. Bacteria then tumble in order to change direction. Experiments have shown that bacteria in environments of high concentration of some attractant...

Cells as Random Walkers

Model

The goal is to simulate a connected, one-dimensional chain of freely diffusing cells. We model the chain of cells by only worrying ourselves with the edges of each cell since we are interested...

Competance in Bacteria

Competance is a state in which bacteria can take in DNA from the environment and add it to their own. It is a desperate action in attempt to speed up evolution in order to survive.

We...

Repressilator

A repressilator is a feedback loop in which each gene suppresses the next one. The following diagram shows an implementation of a repressilator.

Questions about the repressilator

1. When does the repressilator oscillate...

Feedforward Loops

Recall the different types of feedforward loops. Last lecture we discussed the behavior of the C1 loop. The advantage of the C1 loop is that it protects Z from turning on due to fluctuations in X. This...

Network Motifs

We have already examined the one node motif of auto-regulation, let’s now explore 3 node motifs.

Let \(n\) be the number of nodes and \(g\) be the number of edges. For a 3 node motif \(n=3\) and...

Cell Volume as a function of Alpha

Model

A simple check that the simulations are working is to see how the cell volume \(V_j\) changes as \(\alpha\) changes.

We expect that for large...

Autoregulation (continued)

Can we say something quantitative about…

1. Noise reduction for autorepression.
2. Switching time for auto-activation.

Last lecture we came up with an expression for the steady-state probability distribution for an autoregulating protein, but the expression was...

Autoregulation

We will continue our discussion of autoregulating genetic networks. Specifically, we will continue talking about autorepression.

Autorepression

Recall that there are two advantages of autorepression.

1. Reduces response time.
2. Buffers fluctuations.

Noise Reduction (buffer fluctuations)

Network Motifs

In this lecture we will broaden our scope to a whole genetic network.

We define a motif as a pattern that is over-represented in a network. A pattern is considered to be over-represented by comparing it with...

Noise in Gene Activation

We will continue our discussion of noise in gene activation from the previous lecture.

Last lecture we made a simple model for gene activation and the intrinsic noise in the system. Next we...

Gene Activation

In the previous lecture we discussed a simple model of protein production with an activator.

Now lets consider a more involved model.

Additional Considerations

X has its own dynamics

Gene Networks

Starting with this lecture we will shift our attention in this course. Instead of focusing on physical characteristics of biological systems we will focus on functional control of biological systems.

Here is a simple example of a...

The Algorithm

There are three cases that the code handles.

1. Single cell diffusion
2. Edge cell diffusion
3. General case diffusion

The single cell case is treated as a simple random walk. The edge cases and the...

Double Headed Motors

Experimentally, the speed and the force on a loaded motor were calculated.

Unloaded Motor

In the case of an unloaded motor there is no force.

Molecular Motors

amazing picture. (source)

All motors rectify thermal motion. To make a molecular motor its potential energy \(U(x)\) needs to have one of the two following properties.

1. \(U(x)\) is modulated in...

Dynamic Instability of the Microtubule

What is the timescale of fluctuations? (\(\tau\))

A good guess would be that it depends only on the two rates which we are aware of - the attach and detach rates.

Simulation Set-up

• Reflective boundary on the left.
• Absorbing boundary on the right.
• Cells are always connected, cells may stretch and contract.
  • The number of cells is varied.
  • The amount by which a cell can stretch is varied....

1 Cell Diffusion with No State Switching

$$ P(x|t) $$

Prediction

The probability density for cell location given a time \(t\) should look like a normal distribution. As time increases this prediction becomes less accurate since more...

Dynamics: Filament Polymerization

Polymerization at Both Ends (cont.)

Actin

Unlike microtubules, actin does not have the same critical concentration for both ends. The “\(+\)” end is the side where the filament grows and...

Flagellum Propulsion

What is the efficiency of the flagellum?

We are interested in calculating the efficiency of the flagellum as a means of propulsion for the bacteria. Efficiency is defined as the following:

Bacteria Forward Motion

How do bacteria achieve forward motion?

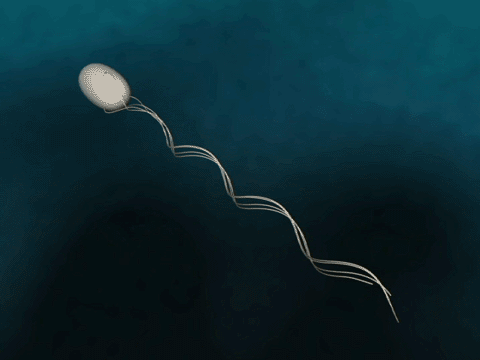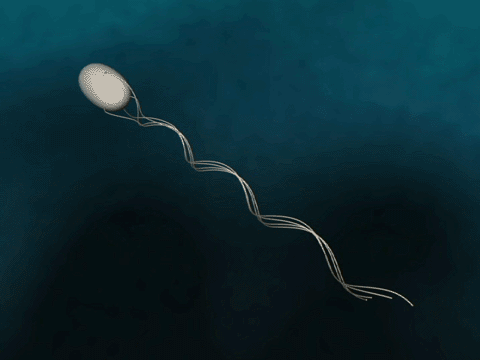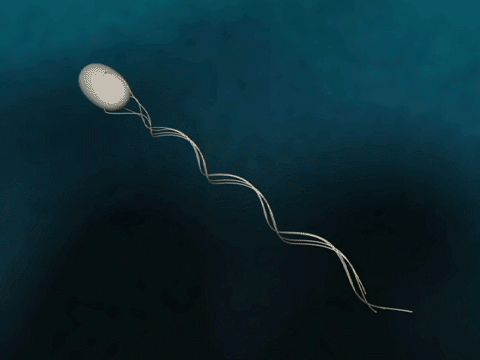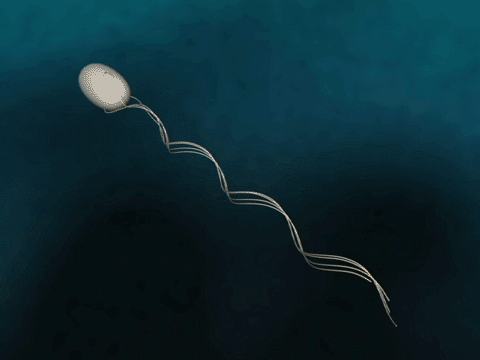source

Bacteria have flagella that drive their propulsion. Bacteria flagella move in a corkscrew pattern. Flagella do not flap back and forth like a paddle....

We will start be continuing in our answer to the question:

What shapes emerge from beinding energy considerations alone?

Pancake

A pancake is a cylinder with rounded sides.

Let the rounded sides have height...

Lipid Geometry

What determines the shape of grouped lipids?

Micelle

A good guess is that conical shaped lipids are more likely to form micelles. Let a cone-shaped lipid have a length \(l\), circular...

Self-Avoiding Chain

• A self-avoiding chain is a freely jointed chain the does not cross over itself.
  • One of the first scientists to work on this problem is Flory.
• We want to quantify how the...

Elasticity (Force-Extension Relations)

Consider a polymer where one end is fixed while the other end is free.

Now we apply a force, \(\vec{f}\), to the free...

Polymers

• In previous lectures we discussed Freely Jointed Chains (FJC) and Freely Rotating Chains (FRC) and derived some properties relating to them.
• We calculated some of the following properties for the FJC and FRC in 3D. Now we...